(c语言x的y次方编程算法)用C语言编程计算数的y次方，实现高效快速的数值计算功能

在计算机科学和数学中，计算一个数的y次方是一个常见的任务，在C语言中，实现这一功能通常依赖于循环或递归，为了提高效率和速度，我们需要采用一些特殊的方法和算法，以下是一篇关于高效快速计算数的y次方的原创文章，共计1577字。

标题：C语言中高效快速计算数的y次方

一、引言

在编程实践中，计算数的y次方是一个基本操作，在图形学、物理学和加密算法中，经常需要计算大数的幂，当指数y非常大时，直接计算会导致效率低下甚至溢出，本文将探讨如何在C语言中高效快速地计算数的y次方。

二、常见方法

1、循环法：最简单的方法是使用循环，每次将结果乘以基数，这种方法易于理解，但效率较低，尤其是当指数较大时。

2、递归法：另一种方法是使用递归，将指数y分解为更小的指数，然后递归计算，虽然递归可以减少乘法次数，但递归的调用开销和栈溢出风险限制了其应用。

三、高效算法

1、快速幂算法：快速幂算法是一种高效的计算幂的方法，其核心思想是将指数y分解为2的幂的和，算法如下：

```c

double power(double base, int exponent) {

double result = 1.0;

while (exponent > 0) {

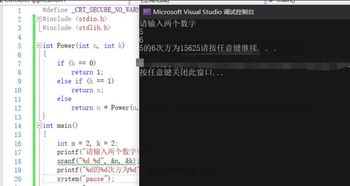
if (exponent % 2 == 1) {

result *= base;

}

base *= base;

exponent /= 2;

}

return result;

}

```

这种方法的时间复杂度为O(log y)，远优于传统的O(y)。

2、矩阵快速幂：对于更复杂的幂运算，如矩阵的幂，可以使用矩阵快速幂算法，这种方法利用矩阵乘法的性质，将幂运算转化为矩阵乘法，从而实现快速计算。

四、分析与比较

1、效率比较：快速幂算法相较于传统方法，在计算大数幂时具有显著优势，计算2的100次方，快速幂算法只需进行大约7次乘法操作，而传统方法则需要100次。

2、空间复杂度：快速幂算法的空间复杂度为O(1)，而递归法可能需要O(y)的空间。

五、常见问题解答（FAQ）

1、问：快速幂算法为什么比传统方法快？

答：快速幂算法通过将指数分解为2的幂的和，减少了乘法操作的次数，从而提高了效率。

2、问：如何处理指数为负数的情况？

答：当指数为负数时，可以计算其绝对值的幂，然后取倒数，计算2的-3次方，可以先计算2的3次方，然后取倒数。

3、问：快速幂算法能否处理浮点数基数？

答：是的，快速幂算法可以处理浮点数基数，只需在算法中适当处理浮点数的乘法即可。

六、结论

在C语言中，通过采用快速幂算法等高效方法，可以快速计算数的y次方，这不仅提高了程序的性能，还减少了资源消耗。

参考文献

1、Knuth, D. E. (1997). The Art of Computer Programming, Volume 2: Seminumerical Algorithms (3rd ed.). Addison-Wesley.

2、Sedgewick, R., & Wayne, K. (2011). Algorithms (4th ed.). Addison-Wesley.

通过以上内容，我们可以看到在C语言中实现高效快速计算数的y次方的方法和重要性，在实际应用中，选择合适的算法和实现方式可以显著提高程序的效率和性能。